개인적인 연구를 진행하던 도중, 어려웠던 개념을 위주로 설명을 간단히 작성한다.

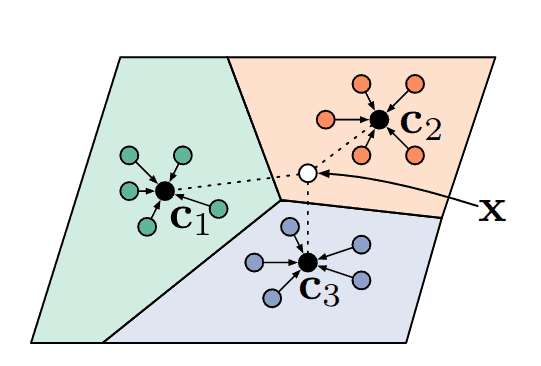
기존 지도학습(Supervised Learning)은 방대한 양의 학습 데이터(A)와 정답 라벨(label)을 기반으로 End-to-End로 학습시키는 수동적인(Passive) 방식을 따른다. 반면에, 능동학습(Active Learning)은 전체 데이터셋(A)에서 신뢰도(모델의 logit, entropy 등)를 기반으로 여러 샘플링(Sampling) 기법을 통해 정보량이 크거나 불확실성이 높은 데이터를 모델이 직접 선택(B)하여, 라벨링하고 학습하는 방식을 뜻한다.
*정보를 기반으로 선택(Selection)을 한다는 점에서 무한한 State-Space를 다루고자 Regularization을 기반으로 탐험(exploration)하는 RL과 유사한 면이 있다.
직관적으로는 쉽지만, 깊게 들어가면 난해해지는 개념이다. 우선 이 개념에 대해 설명하기에 앞서, test데이터가 무엇인지부터 정의하고 가고자 한다. 보통 모델을 학습시킬 때, 엔지니어는 지금까지 수집한 데이터 및 라벨을 train/test/validation set으로 분리하고 train loss와 test/validation accuracy를 기준으로 학습의 성공 여부를 판단한다.
하지만 확률분포 개념을 기반으로 생각해보면, 이 분할(split) 과정에는 편향(bias)이 존재한다.
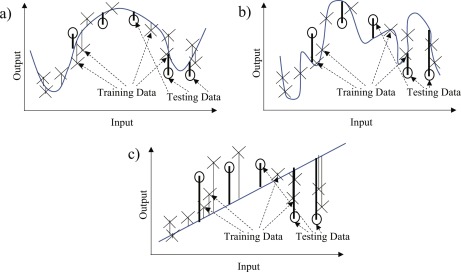
test accuracy나 validation accuracy는 모델의 완벽한 성능을 나타내지 못한다. 위 그림에서 볼 수 있듯이, 전체 데이터(A) 중에서 테스트(B)나 검증(C) 샘플은 전체 모집단 분포 P에 대한 유한 표본이자 추정치($\hat{P}$)이지, 이 표본이 전체 분포를 나타낸다는 보장은 없으며,
일반화에 대한 완벽한 척도가 될 수 없기 때문이다. (물론 현재 많은 Scaling Law에 의존하는 모델들은 이런 문제를 신경안쓰는 듯 하다)
하지만 이보다 더 확실하게 데이터에 대한 학습여부를 나타내는 지표가 아직까지는 없다. 그렇기에 학습과 검증 과정을 분리해서 보지 못한(unseen) 데이터에 대해 검증을 하는 방식을 귀납적(inductive)으로 학습한다고 하며, 많은 모델들의 학습방식이 이 패러다임을 따른다.
반면에 해당 논문에서 소개할 transductive-learning의 경우, test 데이터를 train 데이터와 함께 가지고 학습을 수행한다. 여기서 주의할 점은, test 데이터의 경우 input만 있으며 label이 없는 반면 train 데이터의 경우 label이 있다는 것이다.
label이 없는 학습? train/test가 존재하면 너무 많은 데이터가 있는것이 아닌가? 등의 질문들이 자연스레 떠오르지만, 이는 label에 의한 loss에 의존하지 않고, Sample들의 구조(manifold)를 학습하는 meta-learning이자 metric-learning의 개념으로 보면 된다. 이는 대표적으로 Sample을 기반으로 성능을 향상하는 Few-shot learning과 Test-Time-Training(TTT)및 label-propagation와 아주 밀접한 연관성이 있다.
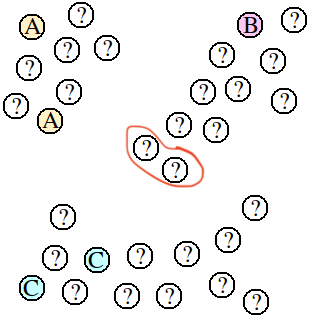
간단하게 다음과 같은 예시를 생각해보자. 위 그림에서 ?로 작성된 node들은 각각 label이 없는 샘플들이다. 이 과정에서 만약 저 빨간색 원에 있는 샘플들을 추론하고자 할때, 해당 공간을 Feature Space로 본다면, 유클리디안 거리에 의해 샘플들은 A나 C로 판명날 가능성이 매우 높다.
하지만 만약에 ?들의 분포(여기서 기억할 점은, ?들은 label이 없다는 점이다.)를 기반으로 두개의 샘플들을 추론하면, 해당 샘플들의 label은 B로 판명나게 될 가능성이 높아진다.
더 자세한 내용은 추후 다른 포스트에서 Learning to propagate labels: Transductive propagation network for few-shot learning(ICLR2019) 논문을 통해 다루고자 한다.