

Recently, i received the Grand Prize Award for Optimizing Large Language Model at Samsung 2025 AI challenge and was awarded with $7,500. Especially, the problem was about expert merging and expert pruning on a Qwen-A3B-30B Model.
But while compressing the model and optimizing the MoE Layer, one question kept nagging on me and after some experiments, the question grew.
"Is there a better architecture(inductive bias), that can outperform Mixture-of-Experts?"
Here are some of my thoughts on what is going on inside this architecture, and what better algorithm could solve this mystery.
Scaling laws have shown that (more parameters ≈ higher performance). So if we want to make our model more powerful, we need bigger parameter space, or bigger matrices.
And to achieve this, Switch-Transformers, Qwen, Deepseek …, used this architecture called Mixture-of-Experts, and many papers have shown that this architecture achieved a big leap in pursuing the Scaling laws. But actually, (in my opinion) this was not a new inductive-bias from the original transformers, but another optimization technique to the transformers.
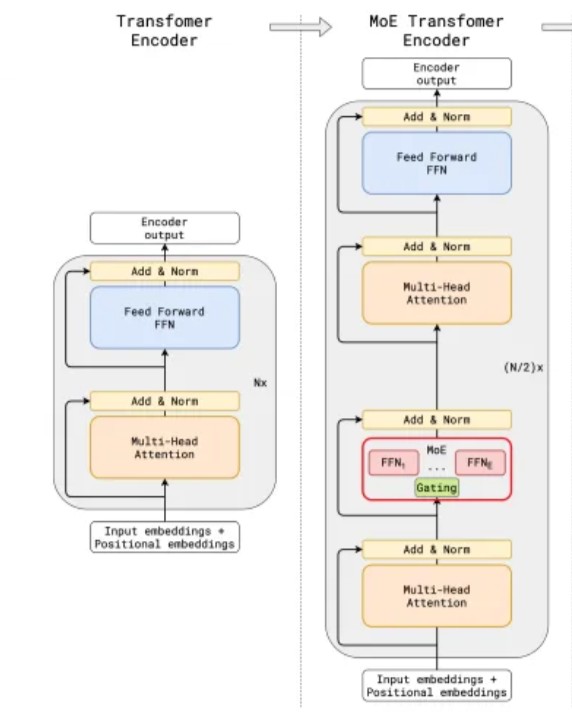
GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding
To me, i think this optimization worked so well for two reasons.
1) The original FFN was originally very sparse, meaning that there was a chance of deviding the Big Matrix(function) into smaller sub-networks. (More superposition)
2) This architecture was so hardware-friendly, meaning that computation costs decreased so well to ignore the VRAM costs.
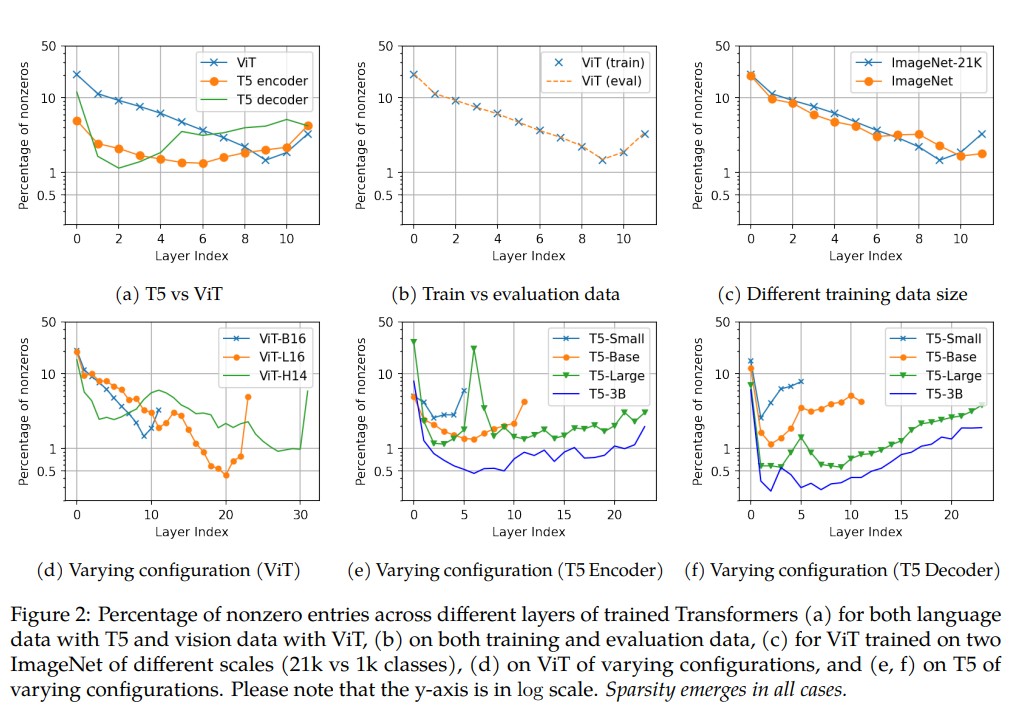
This post will focus more on the first characteristic of FFN.
I think the most important feature addressing this architecture is sparsity. But why does this sparsity even happen? There are many reasons for this such as residual-learning and gradient, but on this post i will focus on a more transformer related reason, which is Attention.
Nikolas Adaloglou’s writing on Why multi-head self attention works: math, intuitions and 10+1 hidden insights tells a very important feature of what the FFN did. This work shows that softmax computation is low rank in-itself.
\[P = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)\]The softmax is applied to the input vectors(or residual stream) to choose which value token must have more information(attention).
\[\begin{array}{cccc} & \langle \text{head 1} \rangle & \langle \text{head 2} \rangle & \cdots \\[6pt] \text{I} & [\,0.3\;\;0.2\;\;0.1\,] & [\,0.8\;\;0.8\;\;0.8\,] & \cdots \\[8pt] \text{think} & [\,0.3\;\;0.4\;\;0.4\,] & [\,0.1\;\;0.1\;\;0.1\,] & \cdots \\[8pt] \text{about} & [\,0.4\;\;0.4\;\;0.5\,] & [\,0.1\;\;0.1\;\;0.1\,] & \cdots \\[4pt] \vdots & \vdots & \vdots & \\[-2pt] \end{array}\]Let’s say the model is trying to predict what comes after “I think about _”. Looking closer at head #2, assuming that the head focuses on nouns and person detection, the softmax computation puts more attention into the value vector of the token [I]. It seems reasonable and a good mechanism for sequence modeling. But what if this massive attention towards token [I] happend at layer 2~3?
If another attention layer comes right after this computation, and another and another.. it seems quite obvious that the predicted next token will only have information about the token [I], which would lead to a sentence like “I think about I I I I …” and so on.
But this kind of behavior almost never accurs in LLMs, because of 2 reasons(or maybe more).
First, the Multi-Head Attention enables the model to learn and express more reach behavior, where each head learns different feature from another. More information or studies could be found in Transformer circuits by Anthropic.
Second, the Feed-Forward-Network works as a information storage, which performs a kind of key-value search in the models parameters to enrich the vectors’ features. This kind of interpretation is shown in the papers Transformer Feed-Forward Layers Are Key-Value Memories.
Another more mathematical interpretation shows that this network as a Rank Restoration procedure in the paper Attention is not all you need: pure attention loses rank doubly exponentially with depth.
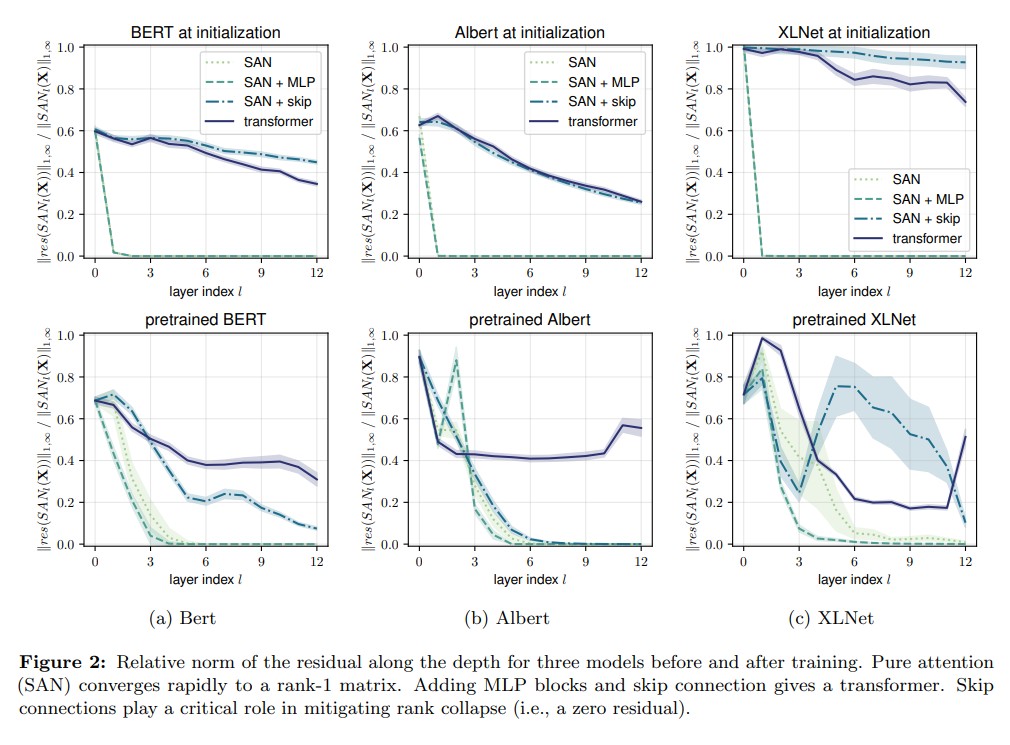
A figure from the paper above which shows the rank destortion as layers go deeper.
In my opinion, although not right in mathematical terms, sparsity is a form of low-rank, since in terms of information, these two terms means that information is low. In other words, sparsity is a form of low-rank caused by the attention layers, and to restore this sparsity the FFN in itself shows a form of sparse network.
Just a idea not experimented. But is there a way to see the attention-sparsity as a null-space of attention?
So this Feed-Forward-Network input is sparse, due to the sparsity that the softmax function has inside the attention layer. And of course, the non-linear functions inside this network as ReLU or GeLU that encourages more sparsity in the FFN’s output due to it’s cut-off functionality.
But this sparsity showed another propety which showed posibilities towards more optimization, which in my opinion, is the key towards finding a better inductive-bias than MoE. This sparsity worked as a way of implicitly expressing more superposition in the neurons of the Transformer architecture.
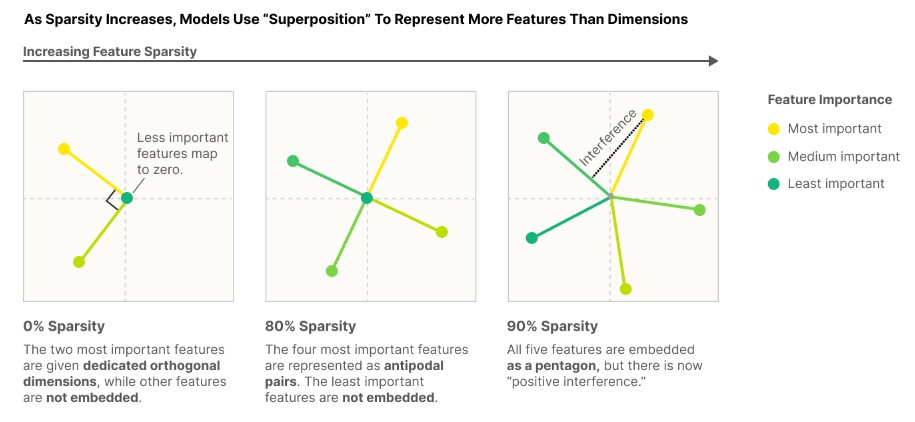
From the Toy Models of Superposition article by Anthropic.
This superposition hypothesis is well described in the blog Toy Models of Superposition by Anthropic. The figure above shows the idea behind superposition, which is that dense output vectors could not express larger feature than the dimension of the vector F, while sparse output vectores could express more features than the dimension due to the superposition characteristic.
It was quite counterintuitive for me at the beginning and still is, but here is what i think is happening. A dense feature vector say
$f$ and a sparse vector $f’$. Since a feature vector must be distinct from one another for a model to detect differnet features from a sequence, it is plausible to say that the features must be sort of $orthogonal$. And a dense feature $f$ has fewer $orthogonal$ or $\text{orthogonal-like}$ features from sparse vector $f’$, the model could express more features than the dimension(basis) when the vector is sparse.
Formally: let the feature directions be \(V=[v_1,\dots,v_F]\in\mathbb{R}^{d\times F},\quad \|v_i\|_2=1,\quad x=Va.\) If a feature vector must be distinct from another, it suffices that active directions can be separated by simple scoring; define the mutual coherence \(\mu := \max_{i\ne j}\, |v_i^\top v_j|.\)
For a (\(k\))-sparse coefficient (a) (i.e., (|\(a\)| = \(k\) « \(d\))), with nonzero entries of magnitude (c>0), we have
\[\underbrace{\langle x, v_i\rangle}_{i\in \mathrm{supp}(a)} \;\ge\; c - \mu (k-1)c, \qquad \underbrace{|\langle x, v_j\rangle|}_{j\notin \mathrm{supp}(a)} \;\le\; \mu k c.\]Hence a simple top-(k) (or threshold) rule correctly recovers the active set whenever
\[c - \mu (k-1)c \;>\; \mu k c \;\;\Longleftrightarrow\;\; 1 \;>\; \mu (2k-1). \tag{f}\]In words: sparser outputs (smaller (k)) tolerate more non-orthogonal (‘orthogonal-like’) directions (larger (F)) in the same (d)-dimensional space, because separation remains valid under the above bound; combinatorially, the number of distinct supports with (\(\le\) k) actives is
\[\sum_{j=1}^{k} \binom{d}{j},\]easily exceeding (d) even for moderate (k). By contrast, dense outputs (large (\(k \approx d\))) violate (\(1>\mu(2k-1)\)) unless the directions are nearly orthogonal, effectively forcing (\(F \lesssim d\)). Therefore, while dense (f) affords fewer orthogonal/orthogonal-like distinguishable features, a sparse (f’) can express more features than the dimension via superposition under the coherence condition above.
And more, i think this comes from the many layers of Multi-Head(Attention) process, where each heads perform there softmax in different dimension in the vector, and aggregate with a Output Matrix. Need more verification with QK curcuit and OV curcuits…
Finally, the characteristics of sparse features above imply that only a few directions are active per input, and superposition means that many directions are available overall. Under this regime, inputs that share similar support patterns cluster in the router’s gating space, so even a simple router can conditionally separate them with a Top-𝑘 k rule.
Therefore each selected expert then specializes on a low-interference subspace, reducing gradient conflict and improving capacity utilization. But although theoryatically this sparsity have enabled the router to succesfully locate subspace, this explicit way of deviding subspace have some issues.
Looking back at the original Vanilla FFN, the wording $\text{top-k}$ was originally used to inidicate the amount of activated neurons in the hidden states after the activation function (ReLU or GeLU).
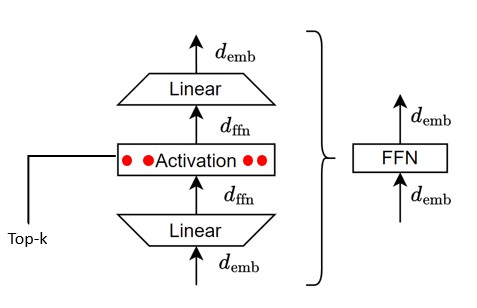
Top-k in FFNs
The Lazy Neuron Phenomenon: On Emergence of Activation Sparsity in Transformers
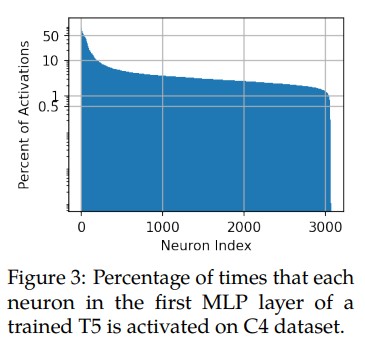
This meant that while performing key-value search for information (see the Second part of Rank Loss), the original FFN used top-k as a computational efficiency term, using very few neurons. This was enabled since the Network already showed a very high sparsity rate in neurons across many architectures and layers (near $\text{3.5%}$).
The Lazy Neuron Phenomenon: On Emergence of Activation Sparsity in Transformers
This meant that the $FFN_{\text{up_proj}}$ Matrix had a tendancy to shut-off most neurons (negative bias and enforced zeros), which could be seen in the figure above where there are Generalized neurons with over 50% activation, and Specialized neurons with 5~30% activation.
This was one of the key factors that enabled me to optimize the MoE architecture at Samsung AI Challenge. Experts also showed same tendencies, meaning that implicit neurons were made explicit by experts.
But here lies a very important difference between the $\text{top-k}$ in FFNs and $\text{top-k}$ in MoEs. The $\text{top-k}$ in FFNs is a 1) post-hoc selection of features in the 2) full feature space, meaning that while training the model, no selection occurs.
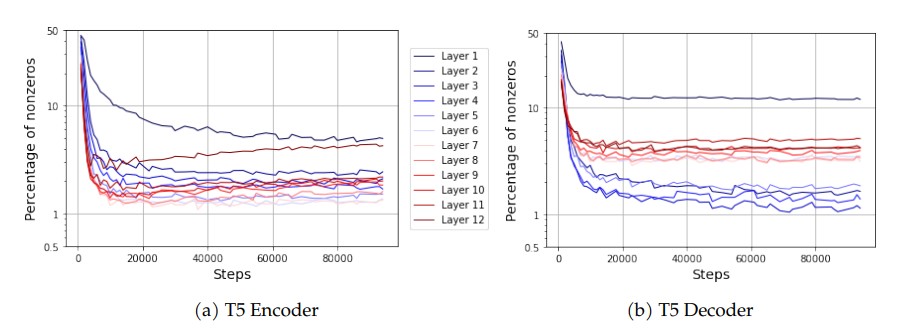
The Lazy Neuron Phenomenon: On Emergence of Activation Sparsity in Transformers
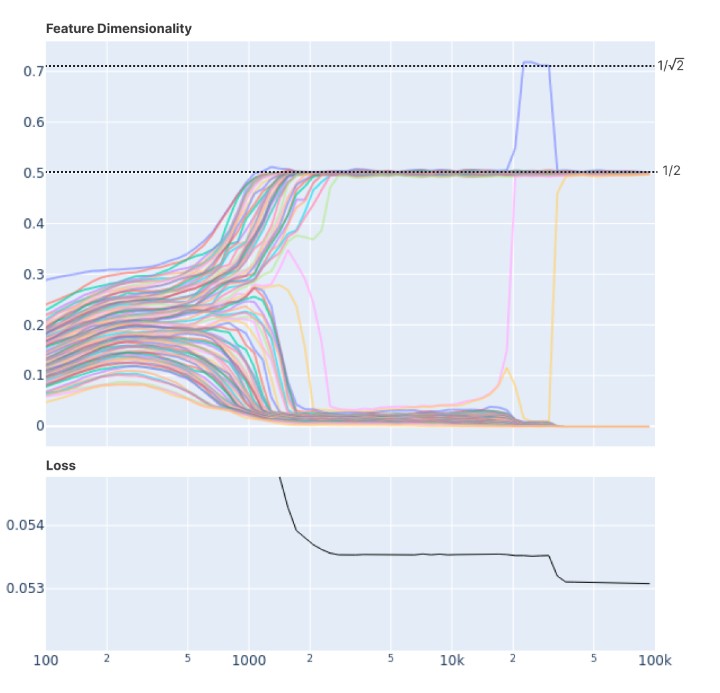
Toy Models of Superposition
The above figures show that feature sparsity, the characteristic that enables this sub-network occurs in the later phase of training. But if the Router tries to select $\text{top-k}$ from the early phase of training, it is likely to cause failure in load-balancing and optimization.
This seems to be delt with in Deepseek-V3, where the authors applied a backpropagation-free method to solve this problem with scoring and bias, but still a heuristic method seem very hard to reproduce.
And of-coures, the original $\text{top-k}$ is done as a method of optimizing a trained FFN, meaning that the $FFN_{\text{up_proj}}$ has trained implicitly to seperate the feature space by calculating all the loss of training samples in the whole space. But the router has less clue about which expert had chosen which part of the feature space (since only $\text{k}$ experts were activated for each sample), meaning that even if the expressioness may have improved, each expert draw the painting without global knowledge.
Many paper deal with this problem with capacity factors, shared experts, Knowledge Distillation and gradient-free methods.
But is there a way that can make a more better inductive bias that is aware of the input-featuers? whether sparse or not?
This part is purely my idea, meaning that it may lack evidence. So it may skip some details on certain parts … Always open for corrections!
Attention is a memory-aware inductive bias in contrast to Markov-Chains. Every time the model auto-regressively outputs a new token, the latent space is updated by Computing $O(N^2)$ tokens every time.
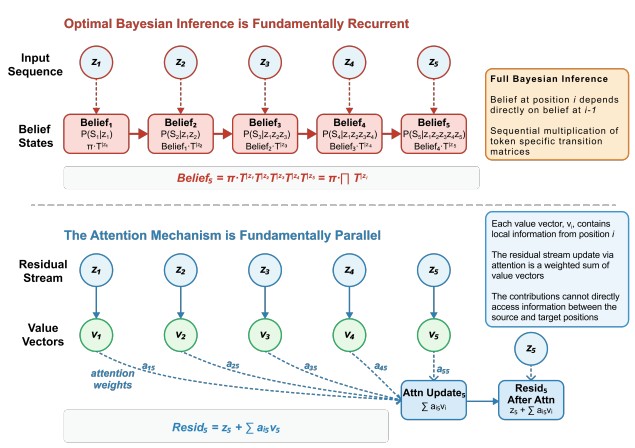
Constrained Belief Updates Explain Geometric Structures inTransformer Representations
Meanwhile, RNNs have a computation complexity of $O(N)$ since the next token only relies on the hidden state at $t\text{-}1$. Either way, both mechanisms have the same objective of updating sequence-state at token sequence $1 \text{~} t$.
On the other hand, the Feed-Forward-Networks and Mixture-of-Experts are sequence-independent. Meaning that the computation taking place in this layer for each token, does not take into account the context in-which the tokens are located (Positional Embedding does encode some time time information).
But why this architecture? I think the biggest reason is computational efficiency. All tokens share the same network to update the residul stream, meaning that it could be done in-parallel with a lot of room for optimization.
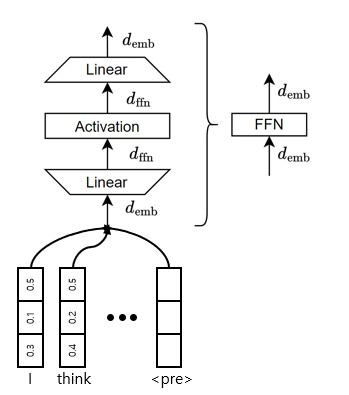
Feed-Forward-Network inside transforemr module
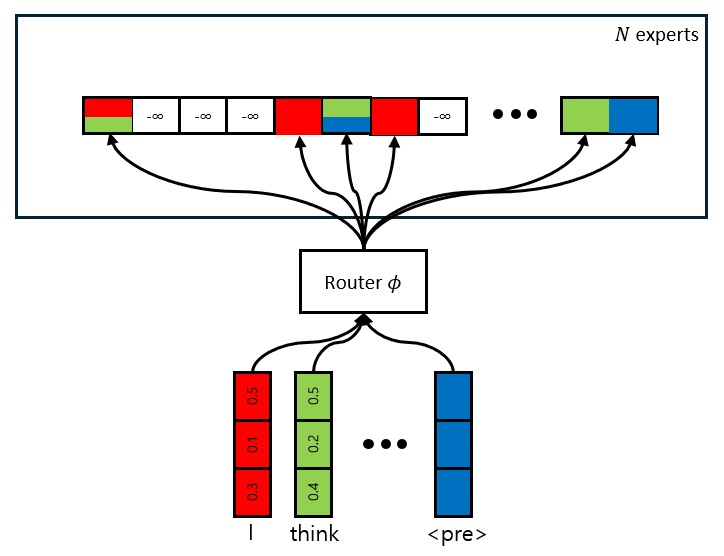
Mixture-of-Experts inside transformer module
Mixture-of-Experts creates a room for more optimization not-only in computation but expressioness. It still does not consider context while performing computation like attention, but it dynamically devides the Large FFN into sub-networks at inference-time, boosting expressivness like the superposition method since sparsity creates more room for orthogonal-like features.
But this kind of “Using subnetworks at inference, increasing the Degree-Of-Freedom” way of Artificial Intelligence is not new. Many know this inductive-bias from the famous paper from Google Deepmind, Conditional Neural Processes. And i think that Neural Process’s inductive bias can be much more suitable than MoE in that it could 1)Devide the large network(function) into sub-networks(surrogate-model) and 2)Efficiently consider context at each auto-regressive NTP(next-token-prediction).
A MoE Layer which has a hyperparameter of $k$ number of experts to choose becomes very hard to optimize 1)in early stages of training and 2)early layers.
1) As shown above, sparsity and superposition that makes the network easier to configure features comes after many iterations of training. But as the network tries to devide the network into fixed number of sub-networks, the load-balancing becomes very hard which could lead to top 10% of experts doing 80% of the work. <- This phenomena was found at Qwen-A3B-30B Model while optimizing at the Samsung AI Challenge.
2) Also, as transformers are also deep-neural-networks, the experts at the early layers showed very similar outputs, meaning that forcing the model to choose $k$ number of sub-network that express similar features may not be a good choice for the network in terms of expressiveness. <- Also found while optimizing Qwen-A3B-30B
A Neural Process, on the other had, could(or perhaps) avoid these optimization problems.
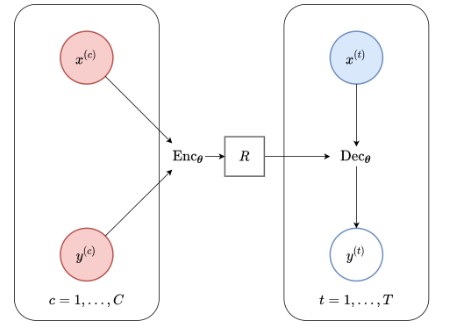
The Neural Process Family from yanndubs.github.io